Calculando velocidades y distancias con el sonido

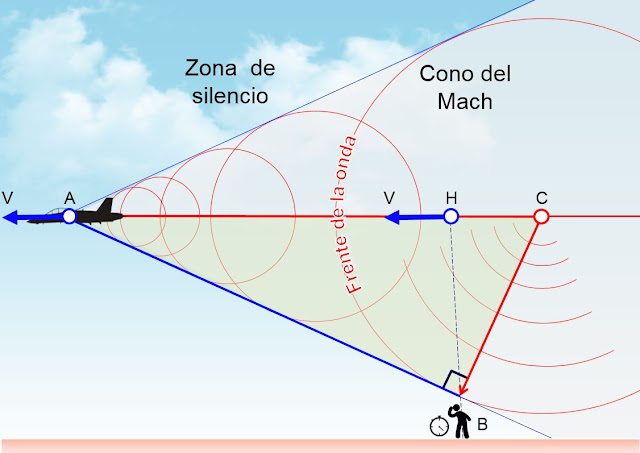
Al volar en régimen supersónico, los frentes de onda van quedando por detrás del avión. Aparece entonces una onda de choque que es una superficie en la cual se produce una discontinuidad. La forma de esta onda de choque la da la superficie tangente a los sucesivos frentes de onda. Si la velocidad del avión es constante, esta superficie es un cono, denominado cono de Mach. Debajo se puede ver una representación de este cono y la geometría que produce.

Internet hay muchos problemas tipo en los que se pide calcular la altura de un avión en base al sonido. Para un piloto ya formado este tipo de problemas no tiene mucho sentido práctico, pero para un aspirante a piloto podría ayudar a entender la trigonometría, que es la base de muchos otros problemas comunes en la vida de un piloto profesional. El siguiente es un ejemplo típico de esos problemas antes comentados que encontré en Internet: 

Un caza F-18 vuela en régimen supersónico horizontalmente a una altura H = 4 km. El estampido nos llega al cabo del tiempo t=10s de haber pasado el avión. Determinar la velocidad v del avión sabiendo que la velocidad del sonido c a la altura del avión es 300 m/s.

Solución:

En la imagen de arriba se puede ver el frente de onda circular que intersecta al observador en el punto B. En el punto C, que es el centro del frente de onda, el avión emitió el sonido. En el punto H el avión pasa sobre el observador. Y cuando el avión llega al punto A, después de 10 segundos de haber pasado por H, el sonido emitido en C llega al observador en B. 

Sea v la velocidad del caza que recorre la distancia HA en el tiempo t=10s, entonces HA = vt. También según el problema la altura BH = h. Por tanto en el gráfico observando el triángulo BHA tenemos que, por el teorema de Pitágoras:

 (1)

Por semejanza de los triángulos BHA y ABC se cumple:

 (2)

El caza emplea el tiempo t en el trayecto del punto C al punto A, es decir la distancia AC es igual al tiempo que el sonido emitido en C tarde en llegar al observador en B. Por tanto tenemos

 (3)

Reemplazando (2) en (3)

 (4)

Igualando (1) y (4)

Donde obtenemos una expresión para la velocidad del avión en función de la altura, la velocidad del sonido y el tiempo. Al conocer todos los datos que nos da el problema, obtenemos una v = 453 m/s. Como era de esperarse la velocidad del avión es mayor que la del sonido.

Leer más: El Boom sónico

Otros artículos