Velocidad de escape

Como se comentaba en el post relacionado con los cañones, parece muy sencillo poner un objeto en órbita. Como se recordará, según el post, bastaba con comunicar a la bala de cañón una velocidad que cumpla con la condición básica de perder 5 metros por cada 8 km recorridos. La cosa en realidad es bastante más complicada.

Si se dispara una bala con suficiente velocidad, el suelo se curva al menos tanto como la bala al caer, por lo que la bala de cañón nunca impacta contra el suelo. Se dice que está realizando una órbita sin interrupción o de circunnavegación. Para cada altura sobre el centro de gravedad hay una velocidad específica que produce una órbita circular.

Para poder establecer estas condiciones, el proyectil deberá desplazarse al menos con una velocidad de 8 km/seg (nada menos). Eso son unos 28.800 km/h. Recuérdese que la velocidad del sonido a nivel del mar en condiciones estándar es de unos 1.200 km/h. Estamos hablando de una velocidad 24 veces mayor, es una velocidad hipersónica. A esta velocidad el simple rozamiento del aire bastaría para reducir  nuestro proyectil a cenizas en unos pocos segundos. Es precisamente por este motivo por lo que el primer paso para poner un satélite en órbita es sacarlo fuera de la atmósfera.

Si prescindiéramos de la atmósfera para simplificar las cosas, veríamos que a medida que cargamos un cañón con más pólvora, aumentaría la velocidad de salida de un hipotético proyectil disparado en el plano horizontal. La órbita se alargaría por el extremo opuesto, convirtiéndose en una elipse. Evidentemente en estas condiciones su elevación sobre el suelo dejaría de ser constante. En el punto más elevado se le llamaría apoapsis y en el más bajo periapsis. En el caso particular de la Tierra se les denomina apogeo y perigeo respectivamente.

Para una velocidad de salida de 9 km/se, la bala describiría una elipse bastante redondeada; a los 10 km/seg el apogeo se desplazaría ya más de 20.000 km de altura; a 11 km/seg el proyectil llegaría hasta mas de medio camino entre la Tierra y la Luna antes de volver atrás; a 11,1 km/seg ya la englobaría dentro de su órbita... Y así ¿hasta cuando?, ¿cuanto más puede "estirarse" esta elipse?

 La verdad es que muy poco más podría alargarse esto. En el momento de alcanzar los 11,2 km/seg se presenta un nuevo y sorprendente fenómeno: nuestro proyectil saldría despedido según una trayectoria no elíptica, sino parabólica. Y una parábola es una curva abierta cuyas ramas se extienden hasta el infinito sin cerrarse jamás. En consecuencia el proyectil no regresaría nunca a la Tierra. Esta velocidad crítica de 11,2 km/seg se denomina "velocidad de escape".

En la ilustración se puede observar el progresivo alargamiento de las órbitas a medida que se incrementa la velocidad inicial, hasta alcanzar el caso límite en la trayectoria parabólica.

En teoría  un vehículo dirigido a Marte  o cualquier otro cuerpo celeste, ha de partir de la Tierra impulsado a esa velocidad. En la práctica podría ser algo menor, puesto que las atracciones gravitacionales de la Luna, de Marte, del sol, etc, también podrían ayudara extraer la nave de la esfera de influencia terrestre; además, la velocidad de escape no es un valor fijo, sino que disminuye a medida que nos elevamos sobre la superficie del planeta. Así, en un disparo efectuado a 200 km de altura, basta con alcanzar los 11 km/seg para garantizar que la nave no volverá a la Tierra. Si cargáramos un hipotético cañón con una cantidad tal que adquiriéramos una velocidad de más de 11,3 km/seg, entonces la trayectoria de escape se convertiría en una hipérbola, que también es una curva abierta, sin retorno al punto departida. Tanto las órbitas circulares como las parabólicas son casos críticos, muy difíciles de alcanzar. Basta una pequeña desviación de las velocidades características para transformarlas en elipses o hipérbolas.

Después de haber visto como poner un satélite en órbita, podemos apreciar que lo más urgente es intentar transportar dicho satélite hasta una altura donde no haya rozamiento con el aire, o bien que este sea mínimo para que la fricción no lo destruya. En la práctica se ha demostrado que un satélite podrá mantenerse en órbita más allá de los 180 km de altura. A menos altura el rozamiento es excesivo. Incluso a la altura de los satélites GPS que están a más de 20.000 km de altura se aprecian efectos del rozamiento. con el tiempo, este pequeño efecto aunque mínimo se nota en los errores de posicionamiento que genera. Errores perceptibles para los precisos relojes atómicos que portan y que debe de ser corregido desde tierra.

Los cohetes portadores constan de una, dos o tres etapas o fases. La primera fase lleva al vehículo hasta una altura no superior a los 100 km; al llegar a ese nivel se apagando los motores y se separa de la segunda fase.  De esta manera se consigue que los motores de esta segunda fase tengan que acelerar sobre una masa menor.
En esta ilustración se puede apreciar la complejidad de la segunda fase del Saturno V. 

A 200 km el satélite tiene garantizada una vida de varios días, o tal vez alguna semana, a esa altura los residuos del aire lo irán frenando poco a poco, haciéndole perder altura paulatinamente. a 500 km de la superficie terrestre un  satélite puede girar durante años; a 1000 km su vida se cuenta ya por siglos. Sin embargo en la realidad estos tiempos se acortan debido a otras circunstancias. Por ejemplo, un satélite de la constelación GPS que podría llegar a costar unos 40 millones de dólares solo tiene una vida media operacional de unos 7 años.

En cualquier caso, incluso estos satélites tan alejados acabarán por sufrir una desaceleración provocada por las pequeñas partículas que todavía se pueden encontrar sueltas en el espacio exterior y acabarán cayendo inevitablemente. Los trozos que vuelvan a reentrar en la atmósfera serán volatilizados debido a la fricción y es muy improbable que un trozo grande de satélite artificial pudiera impactar contra la Tierra.

Momento de la separación de una fase

Hoy por hoy para poder poner un satélite en órbita solo hay un medio: el cohete. Este aparato está diseñado para poder propulsarse en un ambiente sin aire. A través de las distintas fases que van equipadas con su propio combustible, los cohetes se van desprendiendo de estas progresivamente. El satélite suele ir acoplado en el cono de proa o sección de carga, pero en cualquier caso en lo más lato del cohete. El cohete gana velocidad mientras su trayectoria se va haciendo más horizontal hasta ponerse paralelo a la superficie terrestre. Si en ese momento ha alcanzado ya la velocidad para mantenerse en órbita, sus motores pueden apagarse: el satélite ya no caerá.

Después de la separación el cohete seguirá hacia su destino a través de una trayectoria rigurosamente calculada.

¿Por qué se mantienen en órbita un satélite?

La explicación inicial acerca del progresivo "hundimiento" de la Tierra bajo la trayectoria del satélite parece clara, pero no proporciona una respuesta rigurosa. Para poder entenderlo de forma racional, habrá que recurrir a las Leyes de la Gravitación Universal formuladas por Newton en el siglo XVII.

En pocas palabras, un satélite no cae porque en todo momento su peso está exactamente compensado por la fuerza centrífuga que actúa sobre él cuando gira alrededor de la tierra. Si el satélite pesa 100 kg "hacia abajo", deberá de girar a una velocidad tal que la fuerza centrífuga creada sea justamente 100 kg "hacia arriba".

Para que un satélite se mantenga en órbita, debe de girar a tal velocidad que la fuerza centrífuga así generada compense exactamente la atracción que la Tierra ejerce sobre él.

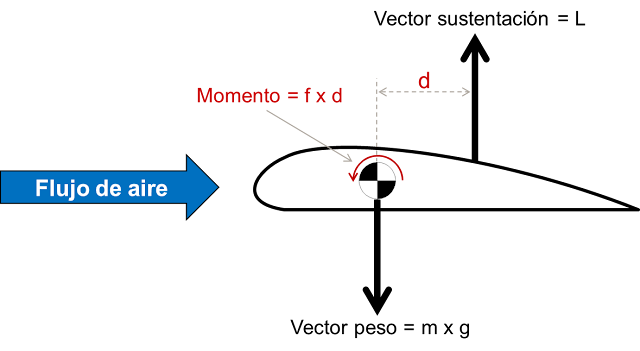
Es algo parecido a lo que pasa con los aviones cuando vuelan recto y nivelado. El peso del avión se compensa produciendo una sustentación igual al peso, pero en sentido contrario.

Sustentación (Lift) y peso (Weight) se igualan, como resultado el avión se mantiene en vuelo.

Pero en el Espacio es algo más complicado, ya que el peso depende de la distancia del cuerpo con respecto al centro de la Tierra. 

En esta imagen se aprecia como cambia el valor de la gravedad terrestre según nos encontremos más lejos o más cerca del centro de la Tierra. En la lanzadera espacial que solía orbitar a unos 400 km de altura, la aceleración de la gravedad es de solo 8,5 m/segundo al cuadrado.

Para saberlo con exactitud no hay más que aplicar la fórmula clásica de la Gravitación Universal, que establece que dos cuerpos se atraen con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que las separa.

A partir de los cálculos relativamente sencillos, se demuestra que la velocidad, v , que debe de tener el satélite para mantenerse en órbita circular a una altura h sobre la superficie terrestre es: 

en la que R y M representan, respectivamente, el radio y la masa de la Tierra y G es la llamada "Constante de la Gravitación Universal" (6.673×10⁻¹¹ N · (m/kg)²).

He aquí el primer resultado interesante: la velocidad que hay que comunicar al vehículo para mantenerlo en órbita depende de la altura de vuelo, pero no de su masa. Un satélite de 200 gramos deberá ir a la misma velocidad que una nave de 100 toneladas situada a igual altura.

Si en la formula anterior se sustituyen los símbolos por sus valores efectivos, resulta que, para un nivel de vuelo de 220 km, la velocidad del satélite ha de ser aproximadamente de 7,7 km/seg. Si ascendemos más, hasta los .1000 km, la correspondiente velocidad para una órbita circular será de 7,4 km/seg. A 10.000 km de altura, bastará con 5 km/seg. De esta forma cuanto más alto vuele un satélite tanto menor será la velocidad requerida para que se mantenga en órbita. En la práctica, el límite de alturas orbitales se alcanza a 1.800.000 km sobre la Tierra. A partir de ahí la atracción solar es predominante, y el satélite, en lugar de girar alrededor de la Tierra, la hace alrededor del Sol. Si en el momento de entrar en órbita terrestre, la componente horizontal de la velocidad es superior a la mínima requerida, se plantea el caso de una órbita elíptica. En general, puede decirse que la trayectoria sería tanto más alargada cuanto mayor sea el exceso de velocidad adquirido, hasta el caso límite  de convertirse en una parábola de escape.

Salvo en el caso de la órbita circular, la velocidad orbital no es constante, sino que varía a lo largo de la órbita, siendo tanto menor cuanto más alejado está el cuerpo que órbita del astro que le atrae. En el caso del movimiento de los planetas en el Sistema Solar cabe destacar tres valores significativos:

• Velocidad orbital mínima es la que corresponde al afelio.
• Velocidad orbital máxima es la que corresponde al perihelio.
• Velocidad orbital media durante un recorrido completo de la órbita.

Las velocidades orbitales se expresan en km/s o en km/h. Suele emplearse el valor de velocidad orbital media. Así, el planeta Tierra tiene una velocidad orbital media de 29,78 km/s.

Navegación de precisión
Después de nueve años y medio y casi 5000 millones de kilómetros de viaje la sonda New Horizons llegó a Plutón 96 segundos antes de lo previsto cuando se planificaba la misión a principios de los 2000.